三角形の相似と複素数

複素平面での三角形の相似

点$\rm{P(\it{z}_1\rm), Q(\it{z}\rm _2\rm), R(\it z \rm _3), P'(\it w \rm_1), Q'(\it w \rm _2), R'(\it w \rm _3)}$に対し

$$\triangle{\rm{PQR}}\text{と} \triangle{\rm{P’Q’R’}} \text{は同じ向きに相似} \Leftrightarrow \frac{z_3-z_1}{z_2-z_1}=\frac{w_3-w_1}{w_2-w_1}$$

同じ向きに相似

$\triangle{\rm{PQR}}\text{と} \triangle{\rm{P’Q’R’}} \text{は同じ向きに相似}$とは…$\\$ $\triangle{\rm{PQR}}$を平行移動，回転移動，拡大・縮小することで$\triangle{\rm{P’Q’R’}}$に重ねることができるときにいう．

なんで，この文が必要なの？

同じ向きに相似の操作にひっくり返す操作がないからそれが原因かな？

いや，ひっくり返す操作については三角形の表記の仕方（頂点の対応）でオッケーじゃない？

では，$\triangle{\rm{PQR}}\text{と} \triangle{\rm{P’Q’R’}} \text{は相似であると仮定すると}$

(i) $\triangle{\rm{PQR}}\text{と} \triangle{\rm{P’Q’R’}} \text{は同じ向きのとき}$

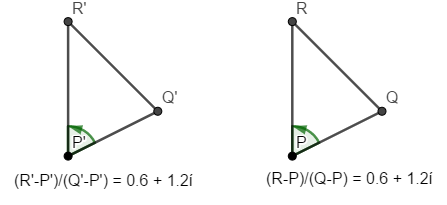
(ii) $\triangle{\rm{PRQ}}\text{と} \triangle{\rm{P’Q’R’}} \text{は異なる向きのとき}$

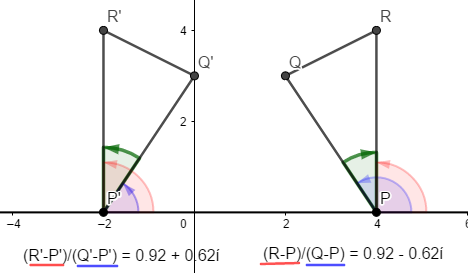
そうか．回転の方向が関係しているのか．面倒だな

逆向きの相似は

$$\triangle{\rm{PQR}}\text{と} \triangle{\rm{P’Q’R’}} \text{は逆向きに相似} \Leftrightarrow \frac{z_3-z_1}{z_2-z_1}=\overline{\left( \frac{w_3-w_1}{w_2-w_1}\right) }$$

一言

二人で向き合って roll．背中合わせに roll．